The mean of the sampling distribution will be equal to the mean of the. However the central limit theorem provides a theoretical basis for why it has wide applicability.
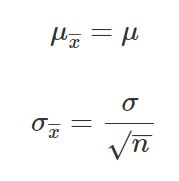
Central Limit Theorem Definition Formula And Applications
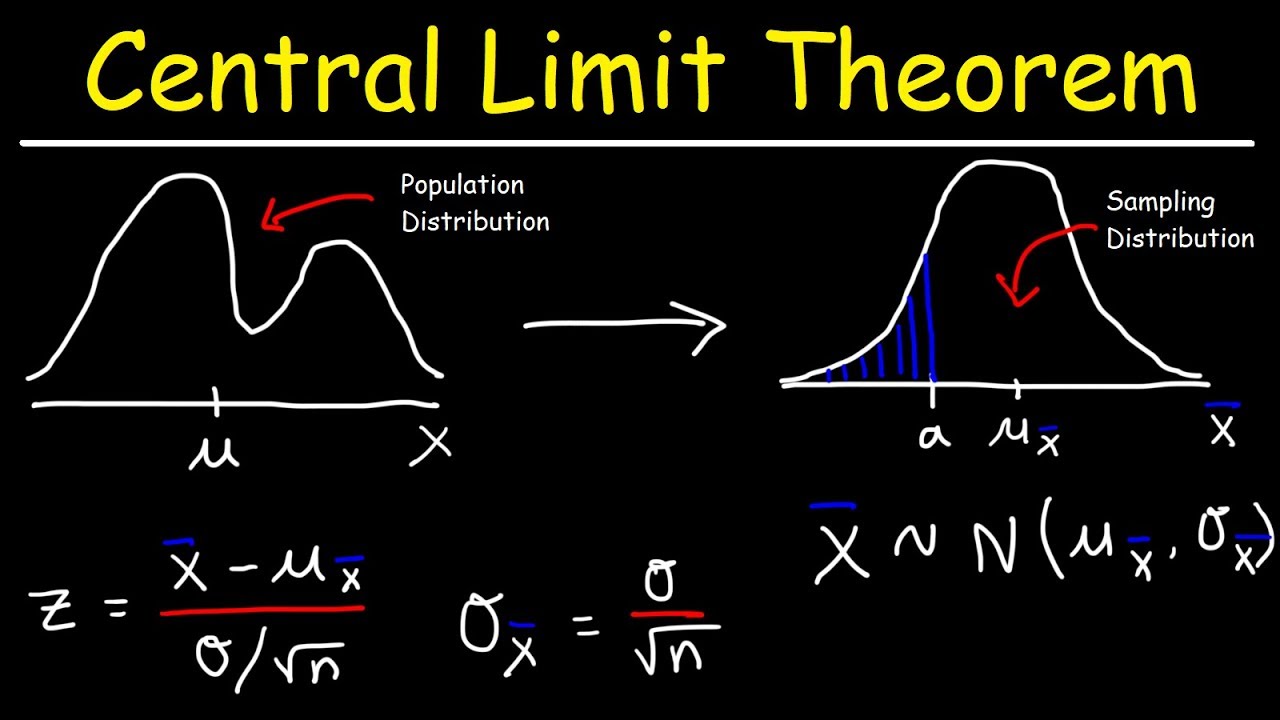
The Central Limit Theorem is the sampling distribution of the sampling means approaches a normal distribution as the sample size gets larger no matter what the shape of the data distribution.
. The central limit theorem states the remarkable result that even when the parent population is non-normal the standardized variable is approximately normal if the sample size is large enough say 30. The central limit theorem is applicable for a sufficiently large sample size n30. The Fourier transform as a tool for solving physical.
If someone has already missed four chances and has to win in the fifth chance then it is a probability experiment of getting the first success in 5 trials. Midrange 435 Explanation. R R be k 1 times differentiable on the open interval with f k continuous on the closed interval between a and x.
The central limit theorem also states that the sampling distribution will have the following properties. Together with a great variety the subject also has a great coherence and the hope is students come to appreciate both. The goals for the course are to gain a facility with using the Fourier transform both specific techniques and general principles and learning to recognize when why and how it is used.
Mean-value forms of the remainder Let f. B is the period so you can elongate or shorten the period by changing that constant. We also provide a Volatility Calculator with a downloadable excel template.
Here we discuss How to Calculate Volatility along with practical examples. Second a conservative central force depends only on the distance r between O. Applications of Central.
An essential component of the Central Limit Theorem is the average of sample means will be the population mean. A is the amplitude. Study with Quizlet and memorize flashcards containing terms like The pages per book in a library have an unknown distribution with mean 319 and standard deviation 22 pages.
It is generally not possible to state conditions under which the approximation given by the central limit theorem works and what sample sizes. The probability of success is given by the geometric distribution formula. It is computed numerically.
Central Limit Theorem Formula. Lets read to understand the different types and examples of this phrase. Midrange 87 2.
One of the main differences in the graphs of the sine and sinusoidal functions is that you can change the amplitude period and other features of the sinusoidal graph by tweaking the constantsFor example. N Sample size. σ x Sample standard deviation.
Then for some real number ξ L between a and xThis is the Lagrange form of the remainder. Similarly for some real number ξ C between a and xThis is the Cauchy form of the remainder. Midrange 54 33 2.
μ x Sample mean. This is a guide to Volatility Formula. A key characteristic of the central limit theorem is that the average of the sample mean and sample standard deviation will approximate the population mean and population standard deviation.
The Midrange is being computed as the average of the maximum and the minimum values present in the data sample corresponds to the measure of central tendency. Examples of Percentage Decrease Formula. A conservative central force F has two defining properties.
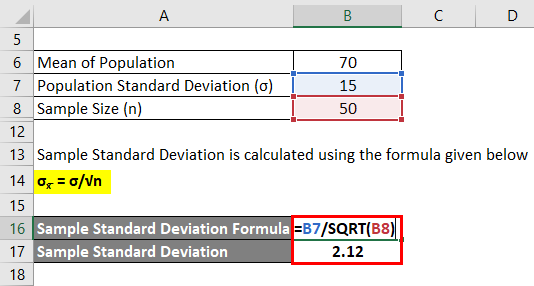
This means that the variable is distributed N. σ Population standard deviation. This free calculator uses the central limit theorem formula to provide step-by-step calculations.
What is the Central Limit Theorem. X n of size n from a distribution with a finite mean and a finite positive variance ² then the distribution of W is N01 in the limit as n approaches infinity. In this article we will learn more about the central limit theorem its formula proof various applications and examples.
The formula for Midrange basically the average of the data set. The formula for the percent point function of the normal distribution does not exist in a simple closed formula. A sample with size n62 was randomly drawn from the population.
Noun a formula proposition or statement in mathematics or logic deduced or to be deduced from other formulas or propositions. The formula for central limit theorem can be stated as follows. First it must drive particles either directly towards or directly away from a fixed point in space the center of force which is often labeled OIn other words a central force must act along the line joining O with the present position of the particle.
The central limit theorem states that the sampling distribution of a sample mean is approximately normal if the sample size is large enough even if the population distribution is not normal. The problem statement also suggests the probability distribution to be geometric. The central limit theorem basically states that as the sample size N becomes large.
A formal statement of the Central Limit Theorem is the following. If is the mean of a random sample X 1 X 2. Using the Central Limit Theorem for Means what is the standard deviation for the sample mean distribution The lengths in inches of.
The central limit theorem states that if the sample size is large enough even if the population distribution is abnormal the sample. Where μ Population mean. You may also look at the following articles to learn more Calculator For Portfolio Return Formula.
Central Limit Theorem Sampling Distribution Of Sample Means Stats Probability Youtube
Central Limit Theorem Definition Formula Examples
Central Limit Theorem Formula Calculator Excel Template
Central Limit Theorem Formula Calculator Excel Template
0 Comments